Table 30 supports the investigation of item bias, Differential Item Functioning (DIF), i.e., interactions between individual items and types of persons. Specify DIF= for person classifying indicators in person labels. Item bias and DIF are the same thing. The item measures by person class are plotted in the DIF Plot.
In Table 30.1 - the hypothesis is "this item has the same difficulty for two groups"
In Table 30.2, 30.3 - the hypothesis is "this item has the same difficulty as its average difficulty for all groups" - this is the best estimate when the data fit the model
In Table 30.4 - the hypothesis is "this item has no overall DIF across all groups"
Example output:
You want to examine item bias (DIF) between Females and Males in Exam1.txt. You need a column in your Winsteps person label that has two (or more) demographic codes, say "F" for female and "M" for male (or "0" and "1" if you like dummy variables) in column 9.
Table 30.1 is best for pairwise comparisons, e.g., Females vs. Males. Use Table 30.1 if you have two classes.
Table 30.2 or Table 30.3 are best for multiple comparisons, e.g., regions against the national average. Table 30.2 sorts by item then person class then item. Table 30.3 sorts by person class then item.
------------------------------------------------------------------------------------------------------------
| KID OBSERVATIONS BASELINE DIF DIF DIF DIF DIF TAP |
| CLASS COUNT SCORE AVERAGE EXPECT MEASURE SCORE MEASURE SIZE S.E. t d.f. Prob. Number Name |
|----------------------------------------------------------------------------------------------------------|
| F 18 18 1.00 1.00 -6.59 .00 -6.59 .00 .00 .00 1 1.000 1 1-4 |
| M 17 17 1.00 1.00 -6.59 .00 -6.59 .00 .00 .00 1 1.000 1 1-4 |
| F 18 16 .89 .92 -4.40 -.03 -3.93 .48 .89 .54 16 .5998 4 1-3-4 |
| M 17 16 .94 .91 -4.40 .03 -5.15> -.75 1.91 -.39 14 .7020 4 1-3-4 |
| F 18 15 .83 .88 -3.83 -.05 -3.22 .61 .79 .77 16 .4504 5 2-1-4 |
| M 17 16 .94 .89 -3.83 .05 -5.14> -1.30 1.90 -.69 14 .5036 5 2-1-4 |
------------------------------------------------------------------------------------------------------------
This displays a list of the local difficulty/ability estimates underlying the paired DIF analysis. These can be plotted directly from the Plots menu.
DIF class specification identifies the columns containing DIF classifications, with DIF= set to @GENDER using the selection rules.
The DIF effects are shown ordered by CLASS within item (column of the data matrix).
KID CLASS identifies the CLASS of persons. KID is specified with PERSON=, e.g., the first CLASS is "F"
OBSERVATIONS are what are seen in the data
COUNT is the number of observations of the classification used for DIF estimation, e.g., 18 non-extreme F persons responded to TAP item 1.
AVERAGE is the average observation on the classification, e.g., 0.89 is the p-value, proportion-correct-value, of item 4 for F persons.
COUNT * AVERAGE = total score of person class on the item
BASELINE is the prediction without DIF
EXPECT is the expected value of the average observation when there is no DIF, e.g., 0.92 is the expected proportion-correct-value for F without DIF.
MEASURE is the what the overall measure would be without DIF, e.g., -4.40 is the overall item difficulty of item 4 as reported in Table 14.
DIF: Differential Item Functioning
DIF SCORE is the difference between the observed and the expected average observations, e.g., 0.92 - 0.89= -0.03
DIF MEASURE is the item difficulty for this class, e.g., item 4 has a local difficulty of -3.93 for CLASS F.
The average of DIF measures across CLASS for an item is not the BASELINE MEASURE because score-to-measure conversion is non-linear. ">" (maximum score), "<" (minimum score) indicate measures corresponding to extreme scores for this CLASS. "E" indicates an extreme score on all items.
DIF SIZE is the difference between the DIF MEASURE for this class and the BASELINE DIFFICULTY, i.e., -3.93 - -4.40 = .48. Item 4 is .48 logits more difficult for class F than expected.
DIF S.E. is the approximate standard error of the difference, e.g., 0.89 logits
DIF t is an approximate Student's t-statistic test, estimated as DIF SIZE divided by the DIF S.E.
d.f. t has approximately (COUNT-2) degrees of freedom excluding observations of extreme persons.
Prob. is the two-sided probability of Student's t. See t-statistics.
These numbers are plotted in the DIF plot. Here item 4 is shown. The y-axis is the "DIF Measure".
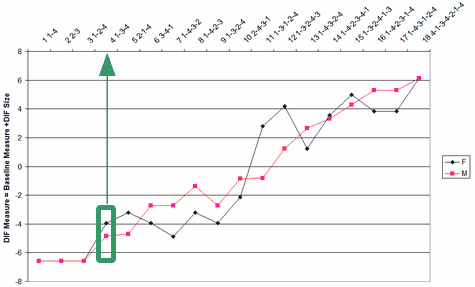Table 31.1 Differential person functioning DPF pairwise
Example 1: Where do I extract appropriate difficulties for my classes for both items that exhibit DIF and those that don't?
The DIF-sensitive difficulties are shown as "DIF Measure" in Table 30.1. They are more conveniently listed in Table 30.2. The "DIF Size" in Table 30.2 or Table 30.3 shows the size of the DIF relative to the overall measure in the IFILE=.
To apply the DIF measures as item difficulties, you would need to produce a list of item difficulties for each group, then analyze that group (e.g., with PSELECT=) using the specified list of item difficulties as an anchor file (IAFILE=).
My approach would be to copy Table 30.3 into an Excel spreadsheet, then use "Data", "Text to Columns" to put each Table column into a separate Excel column. The anchor file would have the item number in the first column, and either the overall "baseline measure" or the group "DIF measure" in the second column. Then copy and paste these two columns into a .txt anchor file.
Example 2: What is the impact of DIF on person measures?
Please look at Winsteps Table 30.2 or 30.3. The average effect of the DIF on person measures of the person group is (DIF Size for the item for the person group)/(total number of items). DIF has raised the person measures if the observed average of the scored responses is greater than expected, and vice-versa.
